Das geozentrische Weltbild war nicht ohne Probleme. Das wussten bereits die alten Griechen. Sie konnten z.B. beobachten, dass die Helligkeit der Planeten nicht immer gleich ist. An Mars lässt sich das gut mitverfolgen. Es gibt Zeiten, da strahlt er auffällig vom Himmel herab.
Einige Wochen später aber ist er relativ unscheinbar und weniger hell als Vergleichssterne wie Antares aus dem Sternbild Skorpion oder Aldebaran aus dem Sternbild Stier, denen er zeitweise sehr ähnlich sieht.
Problem 1: Helligkeitsschwankung bei Planeten
Die Helligkeitsschwankung wurde schon von Ptolemaeus darauf zurückgeführt, dass der Abstand zwischen Erde und Mars nicht immer gleich groß ist. Doch wie bringt man das mit den Kristallschalen in Einklang, an denen nach Vorstellung der Alten Griechen die Planeten befestigt sind? Die Kristallschalen besitzen ja ideale Kugelgestalt, und in deren Mittelpunkt ruht die Erde!
Die große Stunde der Epizykel
Ptolemaeus versuchte das Problem mit Hilfskreisen zu lösen. Er setzte auf den Hauptkreis (Deferent) einen kleineren Hilfskreis (Epizykel), auf dem wiederum der Planet befestigt ist. Der Deferent dreht sich um die Erde und führt den Epizykel mit. Der Epizykel rotiert um die Stelle des Deferenten, an der er mit diesem 'verbunden' ist, und mit ihm bewegt sich der Planet. Der Planet, z.B. Mars, vollführt nun keine Kreisbahn mehr, sondern eine Ellipse, bei der der Abstand Erde - Planet variiert.
Problem 2: Die Änderung des Durchmessers beim Mond
Mit dieser Lösung lässt sich ein weiteres Problem beheben, wenn man es auch auf den Mond anwendet: Der Durchmesser des Mondes ist nicht immer gleich groß. Am deutlichsten wird das bei einer ringförmigen Sonnenfinsternis: normalerweise verdeckt der Mond die Sonnenscheibe während einer Sonnenfinsternis vollständig.
Bei einer ringförmigen Sonnenfinsternis aber ist der Mond zu klein, es bleibt der Rand der Sonne unverdeckt. Die Epizykelvariante würde dafür sorgen, dass der Mond zeitweise näher an der Erde ist und somit größer erscheint, und zeitweise einen großen Abstand zur Erde hat und somit kleiner erscheint.
Problem 3: Die Schleifenbewegung
Verändert man den Durchmesser des Epizykels, lässt sich sogar noch ein weiteres Problem des geozentrischen Weltbildes lösen: die Schleifenbewegung der Planeten. Normalerweise bewegen sich die Körper des Planetensystems alle in die gleiche Richtung.
Von Zeit zu Zeit ist aber eine Rückwärtsbewegung zu beobachten. Die Geschwindigkeit des Planeten vor dem Sternenhintergrund nimmt ab, bis er zum Stillstand kommt.
Anschließend bewegt sich der Planet eine Zeit lang entgegen der üblichen Richtung, bis er wieder zum Stillstand kommt und dann wieder die ursprüngliche Bewegungsrichtung einnimmt.
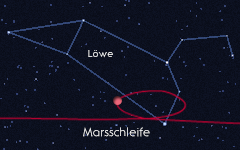
Zeichnet man die Bahn des Planeten auf dem Sternenhintergrund ein, wird eine Schleifenbewegung sichtbar. Besonders deutlich zeigt Mars dieses Verhalten am Sternenhimmel.
Mehr dazu steht auf der Seite 'Mars beobachten'.
Verkleinert man den Durchmesser des Epizykels, ergibt sich eine Schleifenbewegung (probier es aus!). Eigentlich kommt sie dadurch zustande, dass die Erde den Planeten überholt, ihn also zuerst von hinten sieht, dann an ihm vorbeizieht und ihn dann von vorne sieht.
Es verändert sich also einfach nur unsere Blickrichtung, der beobachtete Planet selbst weicht selbstverständlich nicht von seiner nahezu kreisförmigen Bahn um die Sonne ab. Das wusste man aber damals noch nicht, weshalb die Lösung mit den Epizykeln entwickelt wurde.
Nun sind damit drei Probleme einigermaßen geschickt gelöst, aber ein neues Problem ist entstanden: wie lässt sich ein Epizykel an einer Kristallschale befestigen? Und wie befestigt man einen Planeten an einem Epizykel? Dass sich die Planeten frei durch den Raum bewegen, war damals einfach unvorstellbar.
Ein Planet musste an irgendetwas befestigt sein, um sein Herabstürzen auf die Erde zu verhindern. Die Lösung mit Hilfe der Epizykel ist also auch nur eine theoretische Lösung gewesen, in der Praxis wäre so etwas nicht umsetzbar.
